训练 模型仅仅意味着学习（确定）所有权重的良好值以及来自标记示例的偏差。在监督学习中，机器学习算法通过检查许多示例并尝试找到最小化损失的模型来构建模型；这个过程称为 经验风险最小化。

损失是对错误预测的惩罚。那是， 损失 是一个数字，表示模型对单个示例的预测有多糟糕。如果模型的预测是完美的，则损失为零；否则，损失更大。训练模型的目标是找到一组权重和偏差 低的 所有示例的平均损失。例如，图 3 左侧显示高损失模型，右侧显示低损失模型。请注意该图的以下几点：

  • 箭头代表损失。
  • 蓝线代表预测。

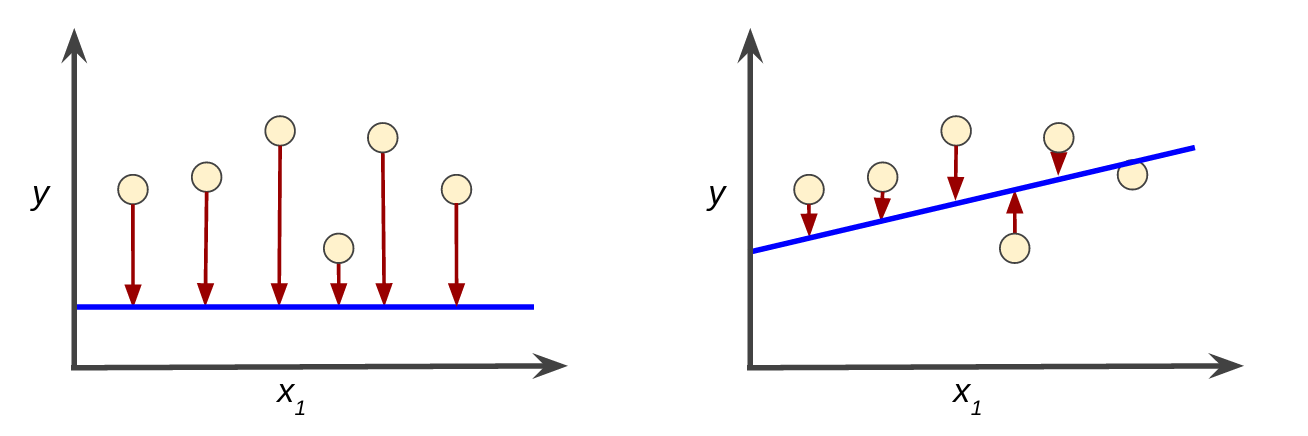
Two Cartesian plots, each showing a line and some data points. In the first plot, the line is a terrible fit for the data, so the loss is high. In the second plot, the line is a a better fit for the data, so the loss is low.

图 3. 左侧模型中的高损失；正确模型的低损耗。

 

请注意，左图中的箭头比右图中的箭头长得多。显然，右图中的线是比左图中的线更好的预测模型。

您可能想知道是否可以创建一个数学函数（损失函数），以有意义的方式汇总各个损失。

平方损失：一种流行的损失函数

我们将在这里检查的线性回归模型使用称为的损失函数 平方损失 （也称为 L2 损失）。单个示例的平方损失如下：

  = 标签和预测之间差异的平方 = (观察值 - 预测(X））2
  = (y - y')2

均方误差 （均方误差) 是整个数据集上每个示例的平均平方损失。要计算 MSE，请将各个示例的所有平方损失相加，然后除以示例数量：

在哪里：

  • \((x, y)\) 是一个例子，其中
    • \(x\) 是模型用于进行预测的特征集（例如，鸣叫声/分钟、年龄、性别）。
    • \(y\) 是示例的标签（例如，温度）。
  • \(prediction(x)\) 是权重和偏差与特征集 \(x\) 相结合的函数。
  • \(D\) 是一个包含许多标记示例的数据集，这些示例是 \((x, y)\) 对。
  • \(N\) 是 \(D\) 中的示例数。

尽管 MSE 在机器学习中很常用，但它既不是唯一实用的损失函数，也不是适合所有情况的最佳损失函数。